Inhaltsverzeichnis
Ein schöner Nebeneffekt des minimalistischen Lebensstils ist, dass man Geld spart und so etwas für die finanzielle Freiheit tun kann. Dabei sind die mächtigen Zinseszinsen nicht wegzudenken. Wenn du sie verstehst, kannst du mit der Zeit reich werden. Jede erfolgreiche Geldanlage baut auf dem Prinzip der Zinseszinsen auf.
Unterschätzt du den Zinseszins, fängst du womöglich zu spät an zu sparen oder startest erst gar nicht.
Doch der Reihe nach: Was ist der Zinseszins einfach erklärt, wie nutzt du die Macht und ist der Zinseszins etwa gefährlich?
Der Zinseszins einfach erklärt
Lege einen Geldbetrag über eine gewisse Zeit an und verzinse ihn. Die Zinsen in Prozent bleiben über die Anlagedauer gleich. Da aber nie Geld entnommen wird, erhöht sich jedes Jahr die Basis, auf der die Zinsen berechnet werden.
Hier ein Beispiel aus der Praxis. Marianne legt jährlich 10.000 Euro an über 30 Jahre bei einem Zinssatz von 5 % pro Jahr. Das Säulendiagramm veranschaulicht die Entwicklung ihres Kapitals:
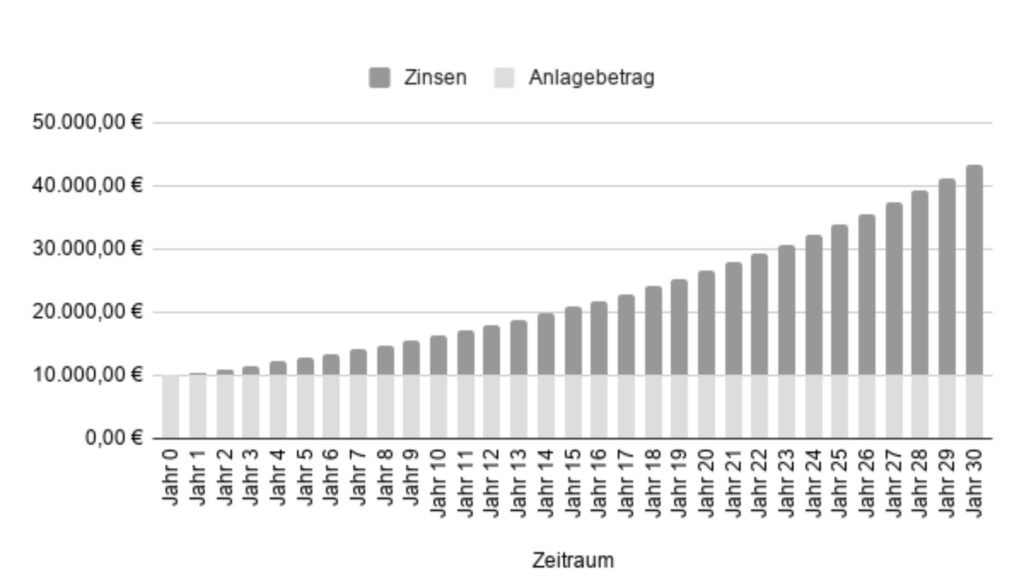
Im 1. Jahr erhält Marianne 500 Euro an Zinsen, also 5 % von 10.000 Euro.
Im 2. Jahr erhält Marianne schon 525 Euro an Zinsen, also 5 % von 10.500 Euro.
Im 3. Jahr erhält Marianne 551 Euro an Zinsen, 5 % von 11.025 Euro.
Nach 15 Jahren übersteigen die erwirtschafteten Zinsen und Zinseszinsen den Anlagebetrag.
Nach 30 Jahren werden mit den ursprünglichen 10.000 Euro ganze 33.219,42 Euro an Zinsen erwirtschaftet. Gesamt besitzt sie jetzt 43.219,42 Euro (exklusive Steuern).
Je länger Marianne das Geld anlegt, desto größer ist die Macht des Zinseszinses. In dem Zusammenhang spricht man auch gerne von einem exponentiellen Wachstum. Das führt zu Ergebnissen, die für uns schwer zu verstehen sind.
Kostenloses Haushaltsbuch

✅ einfach deine Finanzen im Griff
✅ Geld langfristig sparen
✅ Fortschritte sehen
Abonniere den Newsletter und erhalte das Haushaltsbuch kostenlos dazu.
Einfacher Zinseszins-Rechner
Dieser einfache Zinseszins-Rechner dient zur Veranschaulichung und basiert auf der sogenannten Sparkassenformel, mit einer Zahlung des Zinses am 31. Dezember jeden Jahres.
Legende:
K = Startkapital
R = monatliche Sparrate
p = Zinssatz in %
q = 1 + p / 100
n = Jahre
E = Endkapital
Sparkassenformel:

Empfehlenswerte Podcastfolge zum Thema Zinseszins
Das ist ein Platzhalter für den Spotify Player. Um auf den eigentlichen Inhalt zuzugreifen, klicke auf den Button unten. Bitte beachte, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenBeispiele für exponentielles Wachstum in anderen Bereichen
Schon verrückt: so ein einfaches Instrument mit so starkem Wumms! Das exponentielle Wachstum gibt es aber nicht nur in der Finanzwelt.
So vermehren sich Bakterien, und leider auch Viren, exponentiell. Das macht sie so gefährlich.
In der IT gibt es dazu „Moore’s Law“: Das Gesetz besagt, dass sich die Rechnerleistung alle 18 Monate verdoppelt bei gleich bleibenden Kosten.
Diese Verdopplung hat immense Auswirkung auf die Innovationskraft: 1987 wurde der erste Computer für zu Hause verkauft. Der brauchte zwar so viel Platz wie das halbe Arbeitszimmer, aber geschenkt. Zumindest war es möglich, einfache Textdateien zu verfassen. Das war damals schon ein Durchbruch.
10 Jahre später, also 1997, schlug der Rechner „Deep Blue“ von IBM den damaligen Schachweltmeister Kasparow. Unvorstellbar! Gibt es doch beim Schach mehr mögliche Partien als das Universum Atome hat!
Weitere 10 Jahre später präsentierte Steve Jobs das erste Smartphone. Ein Supercomputer im kleinsten Format. Was alles in 10 Jahren bei exponentiellem Wachstum möglich ist!
Wir überschätzen immer die Veränderungen, die in den nächsten zwei Jahren stattfinden werden und unterschätzen die Veränderungen, die in den nächsten zehn Jahren stattfinden werden. Lass dich nicht zur Untätigkeit verführen.
Bill Gates, 1996
Vermögen aufbauen mit dem Zinseszins
Nehmen wir an, Marianne ist 25 Jahre alt und besitzt 5.000 Euro, die sie von ihren Eltern nach erfolgreichem Abschluss erhalten hat.
Marianne legt das Geld in einen breit gestreuten ETF an. Sie findet direkt nach ihrem Studium eine Arbeitsstelle und richtet zusätzlich einen ETF-Sparplan über 250 Euro pro Monat ein. Sie bespart ihre Geldanlage 15 Jahre lang mit einer durchschnittlichen, realen Rendite von 5 % pro Jahr.
Nach den 15 Jahren, wenn Marianne also 40 Jahre alt ist, verfügt sie über 76.882,59 Euro. Dabei hat Marianne gesamt nur 50.000 Euro eingezahlt (monatlicher Sparplan plus 5.000 Euro Geschenk von den Eltern)
Lässt sie den Betrag an der Börse weiter, für sich arbeiten und zahlt keinen Cent mehr ein, dann besitzt Marianne mit 70 Jahren 332.286 Euro! Und das bei nur 50.000 Euro Einzahlung.
Marie macht es anders.
Sie hat die gleichen Voraussetzungen. Nach ihrem Studium erhält sie von ihren Eltern 5.000 Euro geschenkt. Erst mit 40 Jahren investiert sie das Geld an der Börse in einen ETF und eröffnet einen ETF-Sparplan über 250 Euro pro Monat. Das macht sie nicht nur 15 Jahre lang wie Marianne, sondern 30 Jahre lang, bis sie 70 ist. Mit 70 Jahren besitzt Marie bei einem jährlichen Zinssatz von real 5 % 220.926 Euro. Um 111.363 Euro weniger als Marianne, obwohl sie um 45.000 Euro mehr eingezahlt hat: nämlich 95.000 Euro statt 50.000 Euro.

Der wichtigste Faktor ist Zeit. Die Anlagedauer ist sogar wichtiger als der Anlagebetrag! Daher ist es wichtig, schon früh mit dem Sparen zu starten.
Jeder Prozentpunkt mehr Rendite hat Wirkung
Es ist nicht nur die Anlagedauer, die den Zinseszins antreibt. Mindestens genauso wichtig ist die Rendite, also der jährliche Zins, den du für deine Geldanlage erzielst.
Im ersten Beispiel verdoppelt Marianne bei 5 % Rendite nach 15 Jahren ihr ursprüngliches Kapital. Schaffst du es, eine Geldanlage mit 7 % zu finden, dann kannst du dein Kapital in rund 10 Jahren verdoppeln. Im Gegensatz dazu: bei 2 % Rendite brauchst du schon 35 Jahre, bis dein Kapital doppelt so viel wert ist.
Das magische Dreieck der Geldanlage besagt: je höher die Rendite, desto höher das Risiko. Risiken können sich auch eintreten. Börsenkurse brechen ein, die Weltwirtschaft lahmt. Während so einer Baisse gilt es, nicht zu verkaufen und am Ball zu bleiben, damit der Zinseszinseffekt für dich arbeiten kann. Ein häufiges Kaufen und Verkaufen erhöht nur die jährlichen Gebühren und schmälert deinen Gewinn.
Auch wenig Gebühren pro Jahr summieren sich
Zwei Größen arbeiten bei deiner Geldanlage gegen dich und bremsen den Zinseszins: die Inflation und hohe Gebühren.
Du denkst, 1 % mehr Gebühren für deinen Investmentfonds fallen nicht ins Gewicht? Da unterschätzt du den Zinseszinseffekt.
Marianne besitzt bei einer einmaligen Geldanlage von 10.000 Euro und einer realen Rendite von 5 % pro Jahr nach 30 Jahren 43.219,42 Euro. Müsste sie 1 % Gebühren pro Jahr bezahlen für einen Fondsmanager, blieben ihr nur 32.433,98 Euro nach 30 Jahren. Die lächerlichen 1 % Gebühren pro Jahr summieren sich auf 10.785,44 Euro!
Daher achte sogar auf die Nachkommastelle bei Gebühren, die jährlich auf das gesamte Fondsvolumen anfallen. Hier arbeitet der Zinseszinseffekt gegen dich. ETFs sind im Vergleich zu aktiv gemanagten Fonds besonders kostengünstig.
Die Schattenseiten des Zinseszinses
Der Zinseszins hat zwei Seiten. Er kann Vermögen aufbauen und vernichten. Bei Krediten arbeitet der Effekt gegen dich! Selbst bei kleinen Zinsen ist die Auswirkung beträchtlich, wenn du einen hohen Kredit bei geringer Tilgung aufnimmst.
Angenommen, du nimmst einen Kredit über 300.000 Euro auf, um deine Immobilie zu finanzieren. Der Zins von der Bank dafür ist fix bei 1 % über 10 Jahre.
Tilgst du den Kredit bei 3 %, musst du zwar eine monatliche Rate von 1.000 Euro stemmen, nach 10 Jahren bleiben dir nur 205.387,59 Euro Restschuld. Du hast 25.387,59 an Zinsen bezahlt.
Tilgst du den Kredit bei 1 %, musst du zwar nur eine monatliche Rate von 500 Euro bezahlen, nach 10 Jahren bleiben dir jedoch 268.462,53 Euro als Restschuld. Du hast 28.462,53 an Zinsen bezahlt.
Je höher du tilgen kannst, desto weniger Zinsen in absoluten Beträgen musst du für deinen Kredit bezahlen. Daher ist es sehr sinnvoll, wenn du eine Tilgung von mindestens 2 % schaffst und eine jährliche Sondertilgung mit deinem Kreditgeber vereinbarst.
Bei Krediten arbeitet die Inflation tatsächlich für dich. Doch solltest du nicht in Verführung geraten, deswegen ein zu hohes Investment zu tätigen. Die Inflation ist schon in Vermögenswerten wie Immobilien eingepreist.
Ist die Kritik an den Zinseszinsen berechtigt?
So eine Macht provoziert Kritik. Der Vorwurf lautet, der Zinseszins sei nicht moralisch. Er wurde in der Geschichte auch häufig verboten. Im Mittelalter hieß er sogar „Schaden“.
Dem lässt sich entgegen, dass die Zinsen und somit auch die Zinseszinsen Gebühren sind für das Risiko, Geld zu verleihen. Je länger der Kreditgeber auf das Kapital verzichtet (Laufzeit) und je höher das Risiko für einen Ausfall ist (Rendite), desto höher ist der Gewinn.
Kapitalbesitzer gehen ein Risiko ein, wenn sie ihr Geld an Unternehmen verleihen. Der Kreditnehmer könnte insolvent werden. Das Vermögen wäre dann verloren. Ein Ausgleich muss für diese Gefahr gefunden werden. Der Zins bzw. Zinseszins sollte diesen gewähren.
Fazit
Der Zinseszins ist der Turbo für deine Finanzen. Er kann dich reich machen, wenn du früh beginnst, dein Geld anzulegen. Er kann dich auch verarmen lassen, wenn du einen zu hohen Kredit aufnimmst. Nutze ihn, dann wirst du langfristig ein Vermögen aufbauen.
Wie ist deine Einschätzung zum Zinseszins? Habe ich einen Aspekt vergessen? Auf dein Kommentar freue ich mich wieder sehr.





Schreibe einen Kommentar